- The φ-GPU code is a direct N-body simulation code for astrophysics.
- The fully paralelized code uses MPI libraries and contains a native GPU support and a direct code access to the GPU's, by using basic CUDA functions. It uses a "j" particle paralelization as its predecessor (phi-GRAPE code, Harfst et al. 2007 ).
- In its current version, each MPI prozess uses only a single GPU, but two MPI prozesses per node are supported.
- The code uses 4th, 6th and 8th Hermite (H4, H6, H8) integrators, and a Block Individual Timestep Scheme (BITS) in its algorithm (see also Spurzem et al. 2011 (a) for description)
- Due to the hierarchical block time step scheme the average number of active particles Nact (due to a new force computation at a given time) is usually small compared to the total particle number N (but can vary from 1 to N). The full forces are obtained after using the global MPI_Allreduce.
- All the particles are divided equally between the working nodes (using MPI_Bcast) and in each node only the fractional forces are calculated for the, so call, "active" particles at the current time step.
- We use the next table for the number of floating-point operations in force calculation up to potential, acceleration, jerk, snap and crackle
| Max derivative | Total operations | Operation count |
| Potential | 7 add/sub | 4 mul | 1 div | 1 sqrt | 31 |
| Acceleration | 10 add/sub | 8 mul | 1 div | 1 sqrt | 38 |
| Jerk | 21 add/sub | 19 mul | 1 div | 1 sqrt | 60 |
| Snap | 39 add/sub | 38 mul | 1 div | 1 sqrt | 97 |
| Crackle | 61 add/sub | 63 mul | 1 div | 1 sqrt | 144 |
- In the φ-GPU code we mainly use the single precision (SP FP) arithmetics. But in "critical" places, like:
| Calculation of particles separation & relative velocities |
| dr_ij = pos[j] - pos[i] | 3 DP op. = 9 SP op. |
| dv_ij = vel[j] - vel[i] | 3 DP op. = 9 SP op. |
and
| Sumators | |
| pot_i -= pot_ij | 1 DP op. = 3 SP op. |
| acc_i += acc_ij | 3 DP op. = 9 SP op. |
| jrk_i += jrk_ij | 3 DP op. = 9 SP op. |
we emulate the double precision using 2 single precision numbers. So, in these places we need to count for the flops like ~3x more.
- The code is written on CPP and directly uses NVIDIA GPU's via native NVIDIA CUDA compilers & libraries. We use gcc compilers (4.1.2. instead of the default 4.4.2. for our purposes), openmpi (1.4.1- gnu) and CUDA 3.2.
- The code was originaly developed by Nitadori & Berczik. Based on the Nitadori & Makino 4th, 6th & 8th order serial code ("yebitsu") Nitadori, Makino 2008
Submission and running (for DIRAC cluster)
- Interactive jobs: (requests one node and one task per node in the Tesla C 1060), e.g.
fiestas@cvrsvc05> qsub -I -V -A gpgpu -q dirac_int -l nodes=1:ppn=1:tesla
The qsub command creates a new shell running in the user's home directory, e.g.
fiestas@cvrsvc05> ./gpu-4th
- Batch jobs:
use scripts for different Hermite methods (phi-gpu4th.sh, phi-gpu6th.sh, phi-gpu8th.sh)
- For more information, see here:
http://www.nersc.gov/users/computational-systems/dirac/running-jobs/
Performance was tested up to 1M particles and run in parallel regime on up to 40 nodes (DIRAC cluster). The set of tests was done by Fiestas J., Berczik P., Spurzem R. (ARI-ZAH Heidelberg, Germany) & Nitadori K. (RIKEN, Tokyo, Japan). In the following we show benchmarks performed in the Dirac cluster (NERSC) (see also
Spurzem et al, 2011 ).
- Benchmarks up to 40 nodes were performed using H4, H6 and H8 integrators. For performance of the N-body application on NVIDIA GPU cards (φ-GPU code) in the 4th Hermite runs, see following Figures.
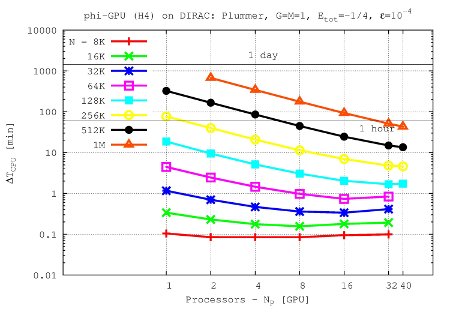 Integration time for 1 NBody unit vs. processor number up to 40 GPU nodes and 1M particles
Integration time for 1 NBody unit vs. processor number up to 40 GPU nodes and 1M particles
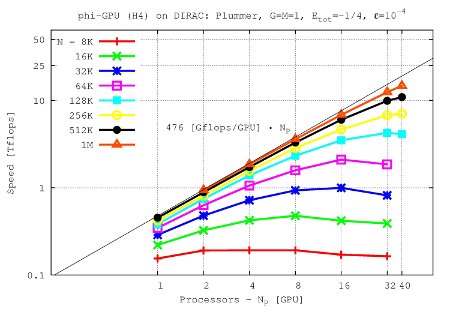 Speed (TFlops) vs. processor number:
Speed (TFlops) vs. processor number:
Results show ~480 Gflops with the 4th order Hermite scheme per one Tesla C2050 GPU. The 6th order scheme obtains ~550 Gflops per one Tesla C2050 GPU, while the 8th order scheme basically have a same performance as a 6th order scheme (~555 Gflops per GPU).
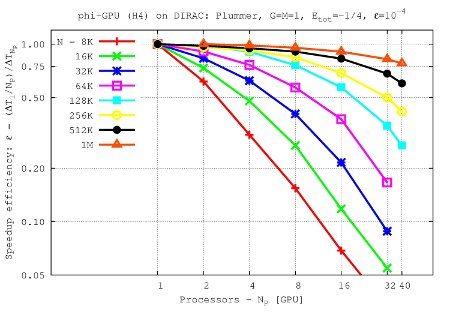 Speedup efficiency (per node) vs. processor number
Speedup efficiency (per node) vs. processor number
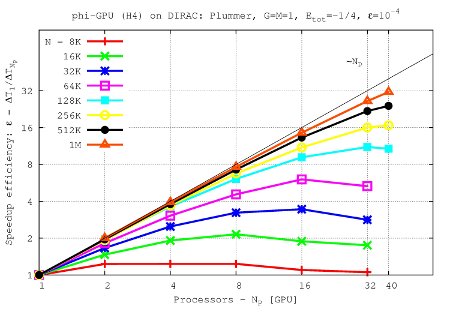 Speedup efficiency (all nodes) vs. processor number
Speedup efficiency (all nodes) vs. processor number
- Figures show T_int (integration time, magenta line) and T_comm (communication time , blue line) vs. node number, in the 4th Hermite runs, and for different particle number N. T_tot=T_int + T_comm is the green line. The optimal processor number is given (approximately) by the intersection of integration and communication times.
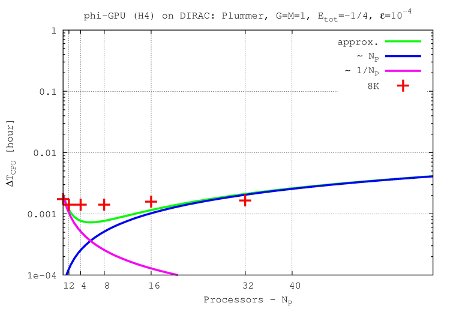 N=8K
N=8K
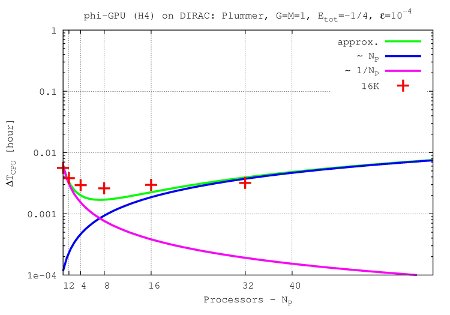 N=16K
N=16K
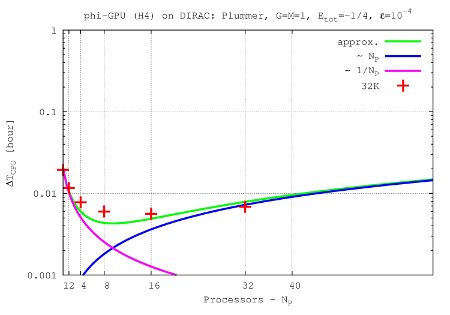 N=32K
N=32K
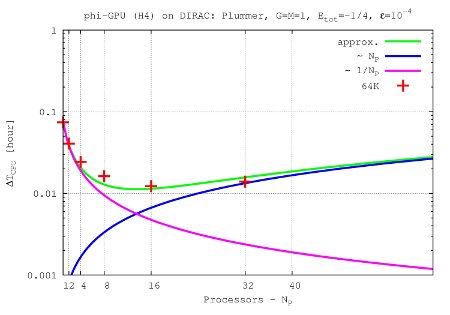 N=64K
N=64K
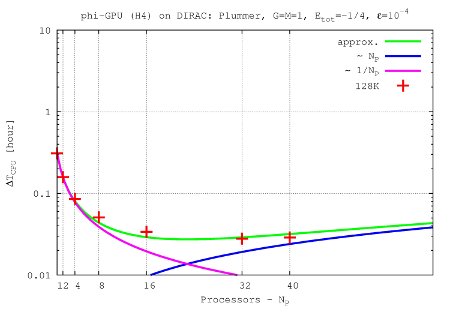 N=128K
N=128K
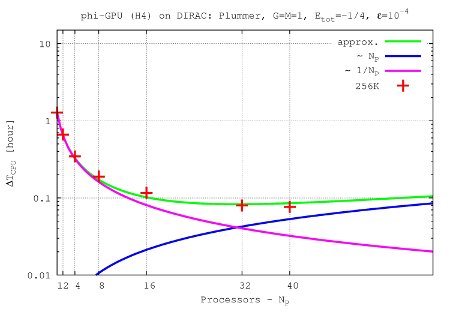 N=256K
N=256K
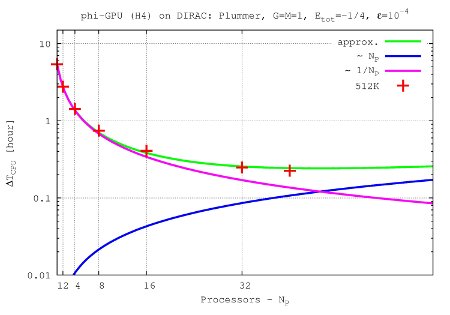 N=512K
N=512K
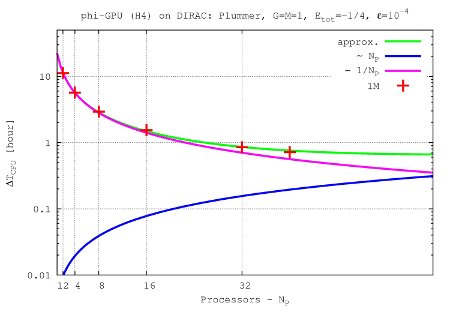 N=1M
N=1M
- Comparison of performance up to 32 nodes in Tesla C2050 (on Dirac cluster) and Tesla C1060 (on Laohu cluster, NAOC, CAS, Beijing, China)
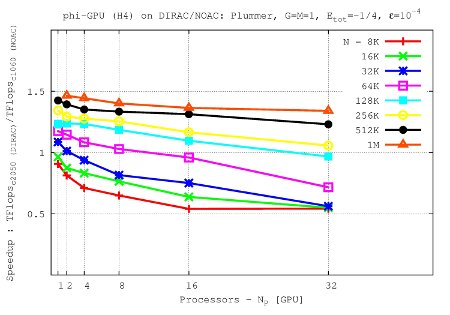 It shows the speedup (TFlops rate) vs node number for the φ-GPU code. Tesla C2050 shows a speed-up up to ~50% (for 1M particles) with respect to Tesla C1060. Integrated for 1 NB time units.
It shows the speedup (TFlops rate) vs node number for the φ-GPU code. Tesla C2050 shows a speed-up up to ~50% (for 1M particles) with respect to Tesla C1060. Integrated for 1 NB time units.
- Comparison of performance bewteen 4-th and 6-th Hermite Scheme in the Tesla C2050 (Dirac cluster)
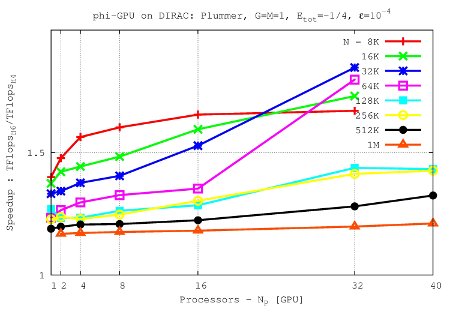 It shows the speed up 6-th Hermite/4-th Hermite (on Dirac cluster) vs node number up to 40 nodes
It shows the speed up 6-th Hermite/4-th Hermite (on Dirac cluster) vs node number up to 40 nodes
- In a first stage the code is prepared to simulate isolated systems with no external field.
- The 'standard' initial conditions are: Plummer sphere, normalization: G=M=1, Etot=-1/4, gravitational softening: ε = 1 x 10-4, integrational parameters for the BITS definition: time step η4th = 0.15, η6th = 0.75, η8th= 1.0. These standard application was used for the benchmarks above.
- Furthermore, we are working in modeling the evolution of a galactic nuclei (GN) embedding a central black hole (BH) in an axisymmetric multi-mass galaxy model. Calculations on the evolutionary time needed to obtaine steady-state density cusps and comparisons to the classical, spherically symmetric, loss-cone theory will be presented in a forthcoming paper. We expect that the inclusion of a heavy BH particle leads to a widespread time-step distribution with very few short stepped particles close to the BH. This hampers scalability and increases the overall integration time compared to the standard benchmarks cases. For a first approach to this problem, using GPUs architectures see Fiestas et al. 2011
References:
- Fiestas, Porth, Berczik & Spurzem , 2011, arXiv1108.3993F
- Harfst, Gualandris, Merritt, Spurzem, Portegies Zwart, Berczik, , 2007,NewA, 12, 357H
- Nitadori, Makino, 2008, NewA, 13, 498 , 2008, NewA, 13, 498
- Spurzem et al., 2011 (a), Computer Science - Research and Development, Vol 26, Num. 3-4, 145-151, ISC'11, Hamburg, Germany
- Spurzem et al., 2011 (b), Accelerated Many-Core GPU COmputing for physics and astrophysics on three continents (2011, submitted to Wiley)

 Integration time for 1 NBody unit vs. processor number up to 40 GPU nodes and 1M particles
Integration time for 1 NBody unit vs. processor number up to 40 GPU nodes and 1M particles Speed (TFlops) vs. processor number:
Speed (TFlops) vs. processor number: Speedup efficiency (per node) vs. processor number
Speedup efficiency (per node) vs. processor number Speedup efficiency (all nodes) vs. processor number
Speedup efficiency (all nodes) vs. processor number N=8K
N=8K N=16K
N=16K N=32K
N=32K N=64K
N=64K N=128K
N=128K N=256K
N=256K N=512K
N=512K N=1M
N=1M It shows the speedup (TFlops rate) vs node number for the φ-GPU code. Tesla C2050 shows a speed-up up to ~50% (for 1M particles) with respect to Tesla C1060. Integrated for 1 NB time units.
It shows the speedup (TFlops rate) vs node number for the φ-GPU code. Tesla C2050 shows a speed-up up to ~50% (for 1M particles) with respect to Tesla C1060. Integrated for 1 NB time units.  It shows the speed up 6-th Hermite/4-th Hermite (on Dirac cluster) vs node number up to 40 nodes
It shows the speed up 6-th Hermite/4-th Hermite (on Dirac cluster) vs node number up to 40 nodes